Leonahard Paul Euler
Leonhard Paul Euler (pron. AFI: [ˈɔʏlɐ] en alemán, AFI: [ˈoɨler] en español) (Basilea, Suiza, 15 de abril de 1707 - San Petersburgo,Rusia, 18 de septiembre de 1783), conocido como Leonhard Euler, fue un matemático y físico suizo. Se trata del principal matemático del siglo XVIII y uno de los más grandes y prolíficos de todos los tiempos.
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculoo la teoría de grafos. También introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del análisis matemático, como por ejemplo la noción de función matemática.1 Asimismo se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Euler ha sido uno de los matemáticos más prolíficos, y se calcula que sus obras completas reunidas podrían ocupar entre 60 y 80 volúmenes.2 Una afirmación atribuida a Pierre Simon Laplace expresa la influencia de Euler en los matemáticos posteriores: «Lean a Euler, lean a Euler, él es el maestro de todos nosotros.»3
En conmemoración suya, Euler ha aparecido en la serie sexta de los billetes de 10 francos suizos, así como en numerosos sellos postales tanto suizos como alemanes y rusos. El asteroide (2002) Euler recibió ese nombre en su honor
PRIMEROS AÑOS :
Euler nació en Basilea (Suiza), hijo de Paul Euler, un pastor calvinista, y de Marguerite Brucker, hija de otro pastor. Tuvo dos hermanas pequeñas llamadas Anna Maria y Maria Magdalena. Poco después de su nacimiento, su familia se trasladó de Basilea al cercano pueblo de Riehen, en donde Euler pasó su infancia. Por su parte, Paul Euler era amigo de la familia Bernoulli, famosa familia de matemáticos entre los que destacaba Johann Bernoulli, que en ese momento era ya considerado el principal matemático europeo, y que ejercería una gran influencia sobre el joven Leonhard.
La educación formal de Euler comenzó en la ciudad de Basilea, adonde le enviaron a vivir con su abuela materna. A la edad de 13 años se matriculó en la Universidad de Basilea y en 1723 recibió el título de maestro de Filosofía tras una disertación comparativa de las filosofías de René Descartes e Isaac Newton. Por entonces, Euler tomaba lecciones particulares conJohann Bernoulli todos los sábados por la tarde, quien descubrió rápidamente el increíble talento de su nuevo pupilo para las matemáticas.4
En aquella época Euler se dedicaba a estudiar teología, griego y hebreo, siguiendo los deseos de su padre, y con la vista puesta en llegar a ser también pastor. Johann Bernoulli intervino para convencer a Paul Euler de que Leonhard estaba destinado a ser un gran matemático. En 1726 Euler finalizó su Doctorado con una tesis sobre la propagación del sonido bajo el título De Sono5 y en 1727 participó en el concurso promovido por la Academia de las Ciencias francesa por el cual se solicitaba a los concursantes que encontraran la mejor forma posible de ubicar el mástil en un buque. Ganó el segundo puesto, detrás de Pierre Bouguer, que es conocido por ser el padre de la arquitectura naval. Más adelante Euler conseguiría ganar ese premio hasta en doce ocasiones
Notación matemática[editar]
Euler introdujo y popularizó varias convenciones referentes a la notación en los escritos matemáticos en sus numerosos y muy utilizados libros de texto. Posiblemente lo más notable fue la introducción del concepto de función matemática,1 siendo el primero en escribir f(x) para hacer referencia a la función f aplicada sobre el argumento x. Esta nueva forma de notación ofrecía más comodidad frente a los rudimentarios métodos del cálculo infinitesimal existentes hasta la fecha, iniciados por Newton y Leibniz, pero desarrollados basándose en las matemáticas del último.
También introdujo la notación moderna de las funciones trigonométricas, la letra e como base del logaritmo natural o neperiano (el número e es conocido también como el número de Euler), la letra griega Σ como símbolo de los sumatorios y la letra  para hacer referencia a la unidad imaginaria.21 El uso de la letra griega π para hacer referencia alcociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.22
para hacer referencia a la unidad imaginaria.21 El uso de la letra griega π para hacer referencia alcociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.22
 para hacer referencia a la unidad imaginaria.21 El uso de la letra griega π para hacer referencia alcociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.22
para hacer referencia a la unidad imaginaria.21 El uso de la letra griega π para hacer referencia alcociente entre la longitud de la circunferencia y la longitud de su diámetro también fue popularizado por Euler, aunque él no fue el primero en usar ese símbolo.22Análisis[editar]
El desarrollo del cálculo era una de las cuestiones principales de la investigación matemática del siglo XVIII, y la familia Bernoulli había sido responsable de gran parte del progreso realizado hasta entonces. Gracias a su influencia, el estudio del cálculo se convirtió en uno de los principales objetos del trabajo de Euler. Si bien algunas de sus demostraciones matemáticas no son aceptables bajo los estándares modernos de rigor matemático,23 es cierto que sus ideas supusieron grandes avances en ese campo.
El número e[editar]
Euler definió la constante matemática conocida como número  como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función
como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función 

 x en el punto
x en el punto  es exactamente 1. Es más, es el número real tal que la función
es exactamente 1. Es más, es el número real tal que la función 

 x se tiene como derivada a sí misma. La función
x se tiene como derivada a sí misma. La función  x es también llamada función exponencial y su función inversa es el logaritmo neperiano, también llamado logaritmo natural o logaritmo en base
x es también llamada función exponencial y su función inversa es el logaritmo neperiano, también llamado logaritmo natural o logaritmo en base  .
.
 como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función
como aquel número real tal que el valor de la derivada (la pendiente de la línea tangente) de la función 

 x en el punto
x en el punto  es exactamente 1. Es más, es el número real tal que la función
es exactamente 1. Es más, es el número real tal que la función 

 x se tiene como derivada a sí misma. La función
x se tiene como derivada a sí misma. La función  x es también llamada función exponencial y su función inversa es el logaritmo neperiano, también llamado logaritmo natural o logaritmo en base
x es también llamada función exponencial y su función inversa es el logaritmo neperiano, también llamado logaritmo natural o logaritmo en base  .
.
El número  puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, unafracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, es como el límite:
puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, unafracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, es como el límite:
 puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, unafracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, es como el límite:
puede ser representado como un número real en varias formas: como una serie infinita, un producto infinito, unafracción continua o como el límite de una sucesión. La principal de estas representaciones, particularmente en los cursos básicos de cálculo, es como el límite:
y también como la serie:
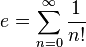
Además, Euler es muy conocido por su análisis y su frecuente utilización de la serie de potencias, es decir, la expresión de funciones como una suma infinita de términos como la siguiente:
Uno de los famosos logros de Euler fue el descubrimiento de la expansión de series de potencias de la función arcotangente. Su atrevido, aunque, según los estándares modernos, técnicamente incorrecto uso de las series de potencias le permitieron resolver el famoso problema de Basilea en 1735,23 por el cual quedaba demostrado que:
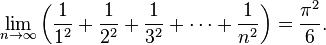
JDC

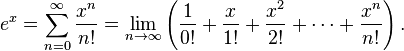
No hay comentarios:
Publicar un comentario