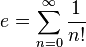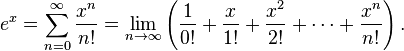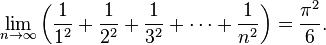El astrolabio es un antiguo instrumento que permite
determinar la posición de las estrellas sobre la bóveda celeste. La palabra
astrolabio procede etimológicamente del griego ἀστρολάβιον,1 que puede
traducirse como «buscador de estrellas». Los marineros musulmanes a menudo lo
usaban también para calcular el horario de oración y localizar la dirección de
La Meca. Durante los siglos XVI a XVIII, fue utilizado como el principal
instrumento de navegación, hasta la invención del sextante, en 1750
• 1 Tipología
• 2
Historia
• 3
Descripción
• 4 Notas y
referencias
• 5 Enlaces
externos
Tipología
El astrolabio a lo largo de la historia se ha ido
perfeccionando y diversificando, de esta forma, nos encontramos con diversos
tipos: el astrolabio planisférico diseñado para el cómputo y representación de
las posiciones de los astros en una única latitud, el astrolabio universal
(válido para todas las latitudes), el astrolabio de Rojas, el astrolabio
islámico, el marinero empleado en la localización de buques y el cuadrante
Historia

Astrolabio persa del siglo XVIII.
En realidad, no se sabe bien quien fue el inventor original.
Algunas obras del astrónomo y matemático griego Claudio Ptolomeo, como el
Almagesto, ya describen en el siglo II su construcción y fueron utilizadas por
otros matemáticos posteriores como Hipatia de Alejandría para mejorar sus
cálculos. Se sabe que Hipatia trabajó con su padre, el astrónomo Teón, para
hacer correcciones en el Almagesto de Ptolomeo y construir un astrolabio.
Descripción
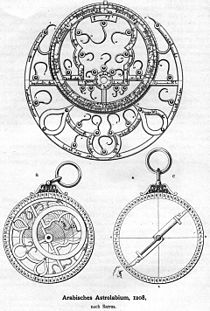
Piezas del astrolabio.
El astrolabio se basa en la proyección estereográfica de la
esfera celeste. Consiste, básicamente, en una circunferencia graduada (placa
madre o mater) sobre cuyo eje gira una aguja con un punto de mira que se apunta
a la estrella elegida. El borde de la madre, o limbo, muestra una escala
graduada en grados y a menudo también otra en horas y minutos. En la parte
superior, consta de una argolla de la que se suspende el instrumento en
posición vertical para realizar las mediciones.
Notas y referencias
1. Volver arriba↑ Astrolabio. Diccionario de la Real
Academia de la Lengua Española
2.Volver arriba↑ Ibn Al-Samḥ (1986). El Kitāb al-ʿamal
bi-l-asṭurlāb (Llibre de l'ús de l'astrolabi) d'Ibn Al-Samḥ: estudi i
traducció. Institut d'Estudis Catalans. pp. 26–. ISBN 978-84-7283-085-1.
Consultado el 17 de noviembre de 2011.
3. Volver
arriba↑
http://www.scribd.com/doc/24820232/Islamic-Science-An-Instrument-of-Mass-Calculation-Nastulus-Baghdad-900-CA
David A. King. Islamic Science - An Instrument of Mass Calculation made by
Nastulus en Bagdad ca. 900 (en inglés). Consultado el 13-03-2010.
Enlaces externos
• Wikimedia Commons alberga contenido multimedia sobre
Astrolabios.
•Wikcionario tiene definiciones y otra información sobre
astrolabio.
•Astrolabios.
•Astrolabios; en inglés.
•Severo Sebojt o Severo de Nísibis (siríaco: ܣܘܪܘܣ ܣܝܒܘܟܬ; Nísibis, 575 - 667): Tratado del astrolabio
planisférico, escrito en el s. VII a partir de textos griegos.
•Texto bilingüe griego - francés,
con introducción y anotaciones en este idioma, en el sitio de Philippe Remacle
(1944 - 2011): trad. De François Nau (1864 - 1931); Imprimerie Nationale [1],
París, 1899.
 para hacer referencia a la
para hacer referencia a la 


 es exactamente 1. Es más, es el número real tal que la función
es exactamente 1. Es más, es el número real tal que la función